ある事象が起きるか起きないか、あるいは、ある事象が生じる回数または量があらかじめ決まっていない、ということはよくあることです。ただ、その確からしさが事前に分かっていることがあり、それを数値で表したものが確率といえます。また生じる変数の各値に対する確率の対応を確率分布と呼びます。今回はその分布の例とそのExcelでの計算方法を説明します。
例えば、サイコロを10回投げて1の目が1回出る確率はいくらでしょう。さらに、2回、3回、…の場合はどうでしょう。1の目が出る回数は0≦x≦10の整数となりますが、xの各値に対する確率はどうなるでしょう。サイコロを投げて1の目が出る確率を1/6とします。実際には、サイコロの各面に掘られている目の数や位置、大きさが違うので、厳密には1/6とはいえませんが、ここでは1/6とします。
上のxの各値に対する確率は二項分布というに確率分布で示されます。二項分布は、一般的に『ある事象が生じる確率がpである操作を同様にn回繰り返すとき、その内x回その事象が生じる確率』を示します。サイコロの例でいえば、1の目が出るのが「ある事象」で、サイコロを振るのが「同様な操作」となります。二項分布は上で述べたn, pの値で規定され、10回サイコロを投げて1の目が出る回数は「n=10, p=1/6」の二項分布に従うことになります。二項分布の数式とExcelの関数は次になります。
二項分布の式 n C x p x(1-p)n-x n C x = n個から x個を選ぶ組合せの数
二項分布のExcelの関数と書式 BINOM.DIST( x , n , p , 関数形式)
二項分布の数式は少し複雑で筆算で計算するとかなりの計算量になりますが、ExcelのBINOM.DISTという関数を使えば、n, pを入力し、上の書式をExcelのセルに入力するだけで簡単に計算できます。関数形式はFALSEまたはTRUEを入力し、FALSEを入力するとxで指定した値をとる確率、TRUEを入力するとxで指定した値以下をとる累積確率が計算されます。
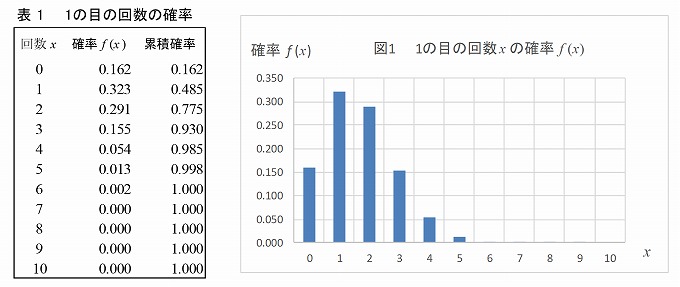
実際にBINOM.DISTを使って、10回サイコロを投げて1の目が出る各回数の確率f (x)は次の表で示されます。図はそれをグラフ化したものです。n=10, p=1/6の二項分布です。
例えば、サイコロを10回投げて1の目が1回出る確率はいくらでしょう。さらに、2回、3回、…の場合はどうでしょう。1の目が出る回数は0≦x≦10の整数となりますが、xの各値に対する確率はどうなるでしょう。サイコロを投げて1の目が出る確率を1/6とします。実際には、サイコロの各面に掘られている目の数や位置、大きさが違うので、厳密には1/6とはいえませんが、ここでは1/6とします。
上のxの各値に対する確率は二項分布というに確率分布で示されます。二項分布は、一般的に『ある事象が生じる確率がpである操作を同様にn回繰り返すとき、その内x回その事象が生じる確率』を示します。サイコロの例でいえば、1の目が出るのが「ある事象」で、サイコロを振るのが「同様な操作」となります。二項分布は上で述べたn, pの値で規定され、10回サイコロを投げて1の目が出る回数は「n=10, p=1/6」の二項分布に従うことになります。二項分布の数式とExcelの関数は次になります。
二項分布の式 n C x p x(1-p)n-x n C x = n個から x個を選ぶ組合せの数
二項分布のExcelの関数と書式 BINOM.DIST( x , n , p , 関数形式)
二項分布の数式は少し複雑で筆算で計算するとかなりの計算量になりますが、ExcelのBINOM.DISTという関数を使えば、n, pを入力し、上の書式をExcelのセルに入力するだけで簡単に計算できます。関数形式はFALSEまたはTRUEを入力し、FALSEを入力するとxで指定した値をとる確率、TRUEを入力するとxで指定した値以下をとる累積確率が計算されます。
実際にBINOM.DISTを使って、10回サイコロを投げて1の目が出る各回数の確率f (x)は次の表で示されます。図はそれをグラフ化したものです。n=10, p=1/6の二項分布です。
次に二項分布を選択問題に応用してみます。例えば10問の四択問題があり、知識が全く無くあてずっぽうに回答するとして、正解数xの確率分布を考えます。n=10で、四択問題なので正解率はp=1/4=0.25となります。よって正解数xは n=10, p=0.25 の二項分布に従います。
10問の内6割以上正解すれば合格とします。したがって「6≦x」が合格となります。この「6≦x」の確率を上のBINOM.DISTで計算すると0.01972となります。あり得ない確率ではありません。ということは、全く知識がなくても彼は合格してしまうかもしれません。これは問題です。
そこで次に問題数を増やして20問として、同様に6割以上の正解で合格とすると「12≦x」が合格となりますが、あてずっぽうに回答して、合格する確率は0.00093となり、奇跡に近い運の良さがないと、合格できません。
このように、問題数が多いほど、全く知識が無くても偶然によって合格してしまう確率を小さくできますですが、このことがExcelによる確率の計算によって分かります(このことは理論的にも一般化できますが)。問題数が多いことにはそのような意味があるわけです。
ところで、ここでもし20問で、全くあてずっぽうに答えp=0.25でも合格したとしましょう。合格率が0.00093なのにです。誰もがどこか腑に落ちないでしょう。このとき、計算の元になった仮定「p=0.25」を否定するのが「検定」という分析の考え方です。実際にはp > 0.25で、実は彼に知識があったか、あるいは人並外れた直感力(超能力?)があったか、などということになります。
計算された確率0.00093がおかしいと判断する基準の値を有意水準と呼びます。この有意水準には0.05や0.01の値が使われます。この検定の論法は「p=0.25」の仮定の下で合格した、という事実から理論的に導かれた合格の確率0.00093が有意水準より小さいと仮定「p=0.25」を否定するのですが、この論法は、ある仮定をして論理的に矛盾を導いて、その仮定を否定する背理法の考え方に近いといえます。
以上はExcelを使った二項分布の計算ですが、次はそれを組み合わせた「たたみこみ」という確率の計算について考えます。
さて、経済学部のビジネス統計分析パッケージでは統計検定の受験を推奨しており、すでに何名か合格者を出しています。この資格検定では35問ほど出題され、合格条件はおおむね100点満点で70点以上とあるので、0.7×35=24.5、つまり25問以上が合格条件といえます。五つの選択肢から一つを選ぶ、五択問題です。
上で述べたように、例えば過去の問題を解いてみて自身の正解率pを予測すれば、二項分布から合格率が予測できます。受験料が必要なので、この予測した合格率をみて受験するか否かを決めるのもよいでしょう。
ただ、統計検定の問題にも易しい問題と難しい問題があります。今ある学生Mがいて、彼はこれまで頑張って統計学を勉強してきたかいがあって、問題の多くを解けるようになったが、それでもまだ一部解くのが難しい問題が残っているとします。そこで、彼にとって得意な問題を問題タイプ1、苦手な問題をタイプ2と分けて合格率を予測するとします。問題のタイプ1とタイプ2に対して、予測正解率をp1 とp2、問題数をn1とn2、正解数をx1とx2とします。なお、少し難しくなりますが、x1とx2が各値を取る確率は独立、つまり確率的に互いに影響しないとします。
xを全正解数、つまりx = x1+x2とすると、合格の条件は「25≦x」となります。この合格条件を満たす確率を計算するのに、二つの異なる変数の和の確率を計算する「たたみこみ」という計算を行います。Excelを使って計算しますが、少し工夫が必要です。詳しい計算方法の説明は省略しますが、2つの変数の確率の積の表と変数の値の和の表を作り、ExcelのSUMIF関数という条件付き合計関数を使いました。
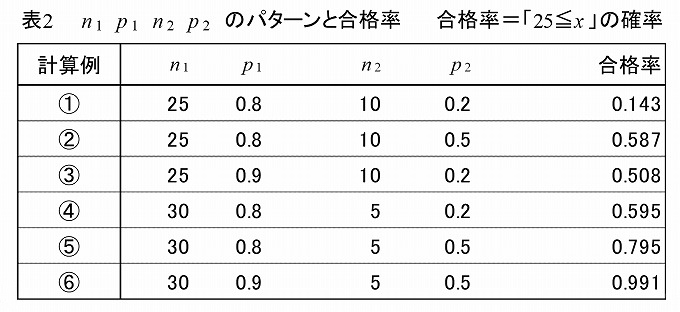
次がn1, p1, n2, p2のいくつか想定したパターンとその計算結果の表です。p2 =1/5= 0.2としたのは、5択で全くあてずっぽうに答えて正解する確率です。
10問の内6割以上正解すれば合格とします。したがって「6≦x」が合格となります。この「6≦x」の確率を上のBINOM.DISTで計算すると0.01972となります。あり得ない確率ではありません。ということは、全く知識がなくても彼は合格してしまうかもしれません。これは問題です。
そこで次に問題数を増やして20問として、同様に6割以上の正解で合格とすると「12≦x」が合格となりますが、あてずっぽうに回答して、合格する確率は0.00093となり、奇跡に近い運の良さがないと、合格できません。
このように、問題数が多いほど、全く知識が無くても偶然によって合格してしまう確率を小さくできますですが、このことがExcelによる確率の計算によって分かります(このことは理論的にも一般化できますが)。問題数が多いことにはそのような意味があるわけです。
ところで、ここでもし20問で、全くあてずっぽうに答えp=0.25でも合格したとしましょう。合格率が0.00093なのにです。誰もがどこか腑に落ちないでしょう。このとき、計算の元になった仮定「p=0.25」を否定するのが「検定」という分析の考え方です。実際にはp > 0.25で、実は彼に知識があったか、あるいは人並外れた直感力(超能力?)があったか、などということになります。
計算された確率0.00093がおかしいと判断する基準の値を有意水準と呼びます。この有意水準には0.05や0.01の値が使われます。この検定の論法は「p=0.25」の仮定の下で合格した、という事実から理論的に導かれた合格の確率0.00093が有意水準より小さいと仮定「p=0.25」を否定するのですが、この論法は、ある仮定をして論理的に矛盾を導いて、その仮定を否定する背理法の考え方に近いといえます。
以上はExcelを使った二項分布の計算ですが、次はそれを組み合わせた「たたみこみ」という確率の計算について考えます。
さて、経済学部のビジネス統計分析パッケージでは統計検定の受験を推奨しており、すでに何名か合格者を出しています。この資格検定では35問ほど出題され、合格条件はおおむね100点満点で70点以上とあるので、0.7×35=24.5、つまり25問以上が合格条件といえます。五つの選択肢から一つを選ぶ、五択問題です。
上で述べたように、例えば過去の問題を解いてみて自身の正解率pを予測すれば、二項分布から合格率が予測できます。受験料が必要なので、この予測した合格率をみて受験するか否かを決めるのもよいでしょう。
ただ、統計検定の問題にも易しい問題と難しい問題があります。今ある学生Mがいて、彼はこれまで頑張って統計学を勉強してきたかいがあって、問題の多くを解けるようになったが、それでもまだ一部解くのが難しい問題が残っているとします。そこで、彼にとって得意な問題を問題タイプ1、苦手な問題をタイプ2と分けて合格率を予測するとします。問題のタイプ1とタイプ2に対して、予測正解率をp1 とp2、問題数をn1とn2、正解数をx1とx2とします。なお、少し難しくなりますが、x1とx2が各値を取る確率は独立、つまり確率的に互いに影響しないとします。
xを全正解数、つまりx = x1+x2とすると、合格の条件は「25≦x」となります。この合格条件を満たす確率を計算するのに、二つの異なる変数の和の確率を計算する「たたみこみ」という計算を行います。Excelを使って計算しますが、少し工夫が必要です。詳しい計算方法の説明は省略しますが、2つの変数の確率の積の表と変数の値の和の表を作り、ExcelのSUMIF関数という条件付き合計関数を使いました。
次がn1, p1, n2, p2のいくつか想定したパターンとその計算結果の表です。p2 =1/5= 0.2としたのは、5択で全くあてずっぽうに答えて正解する確率です。
計算例①を現在の状況とし、p1=0.8で35問中苦手な問題が10問あり、あてずっぽうで答えp2=0.2とすると合格率は0.143となります。以下の計算例の考察では、この計算例①と比較していきます。
計算例②では、苦手な問題を少し克服して、5択から2択に絞り込める力が付いたとしてp2=1/2=0.5とすると、合格率は0.587に上がります。
計算例③では、得意な問題の正解率を0.9に上げたとして合格率は0.508に上がりますが、計算例②ほどには上がりません。計算例②と比較すると、苦手な問題を克服した方が有効だということになります。
計算例④では、得意な問題を30問に増やしたとすると、合格率は0.595に上がります。
計算例⑤では、得意な問題を30問に増やし、かつ苦手な問題の正解率もp2 =0.5にしたとすると、合格率は0.795に上がります。
計算例⑥では、さらに勉強に励んで、得意な問題を30問に増やし、かつ正解率を0.9に上げたとし、さらに苦手な問題の正解率もp2 =0.5にしたとすると、合格率は0.991まで上がります。後は、試験に遅刻しないように気を付けるだけです。
このように、様々な状況・パターンに応じて確率を計算でき、合格率を予想できます。
今回は、確率分布の内、二項分布のBINOM.DISTの利用例を示しました。後半の“たたみこみ”の計算は少し工夫が必要ですが、他の種類の確率分布もそれに対応するExcelの関数を使えば同じように計算できます。その容易さは、昔に比べれば、格段の違いです。その分、より重要なのは各確率分布の意味を理解し、適用・応用できる状況を知ることです。上で紹介したように、身近なソフトであるExcelを使って簡単に各種の確率を計算できるようになりました。様々な状況・現場で利用してほしいと思います。
計算例②では、苦手な問題を少し克服して、5択から2択に絞り込める力が付いたとしてp2=1/2=0.5とすると、合格率は0.587に上がります。
計算例③では、得意な問題の正解率を0.9に上げたとして合格率は0.508に上がりますが、計算例②ほどには上がりません。計算例②と比較すると、苦手な問題を克服した方が有効だということになります。
計算例④では、得意な問題を30問に増やしたとすると、合格率は0.595に上がります。
計算例⑤では、得意な問題を30問に増やし、かつ苦手な問題の正解率もp2 =0.5にしたとすると、合格率は0.795に上がります。
計算例⑥では、さらに勉強に励んで、得意な問題を30問に増やし、かつ正解率を0.9に上げたとし、さらに苦手な問題の正解率もp2 =0.5にしたとすると、合格率は0.991まで上がります。後は、試験に遅刻しないように気を付けるだけです。
このように、様々な状況・パターンに応じて確率を計算でき、合格率を予想できます。
今回は、確率分布の内、二項分布のBINOM.DISTの利用例を示しました。後半の“たたみこみ”の計算は少し工夫が必要ですが、他の種類の確率分布もそれに対応するExcelの関数を使えば同じように計算できます。その容易さは、昔に比べれば、格段の違いです。その分、より重要なのは各確率分布の意味を理解し、適用・応用できる状況を知ることです。上で紹介したように、身近なソフトであるExcelを使って簡単に各種の確率を計算できるようになりました。様々な状況・現場で利用してほしいと思います。
以上